Abstract

Systems for delivering drugs with controlled release have many benefits over traditional dose forms. But because controlled release medication delivery systems are so complex, creating them effectively presents significant hurdles. One method that has been used to create and construct controlled release dose forms is the traditional statistic response surface methodology (RSM). It should be noted that the RSM technique has several limitations. In order to create controlled release dosage forms, a different method known as artificial neural networks (ANN) has recently become quite popular. The fundamental structure of artificial neural networks (ANNs), the creation of ANN models, and an explanation of how to apply ANNs to the design and development of controlled release medication delivery systems are covered in this overview. Sometimes, it's preferable to provide vaccinations. The goal of creating controlled release dosage forms is to keep the drug's concentrations in the blood, target organs, or tissues largely constant. Sometimes, it's preferable to provide vaccinations. Furthermore, the uses of ANNs.

Keywords

Controlled release, Artificial neural network, Deconvolution, Response surface methodology, Formulation Optimization.

Introduction

Overview of medication delivery methods with regulated release:

Advantages over traditional dosage forms are numerous for controlled release drug delivery systems (CRDDS). Localized drug administration, minimal in vivo drug concentration fluctuations and preservation of drug concentrations within a targeted range, enhanced patient compliance, a sharp decline in dose frequency, and fewer adverse effects are a few of these benefits. Research has been done on and a number of controlled release medication delivery methods, including intrauterine devices, transdermal, injectable, oral, and implanted drug delivery methods. But developing controlled release drug delivery systems presents a significant difficulty due to the complexity of formulations needed to maintain the appropriate in vivo drug release rates (1).

The goal of creating controlled release dosage forms is to keep the drug's concentrations in the blood, target organs, or tissues largely constant. Sometimes, it's preferable to provide vaccinations. The loading dose should be released initially in a controlled release drug delivery system, and then the drug's maintenance dose should be released steadily after that. Drug release rates from various delivery systems may fluctuate at different release stages, and the majority of controlled release drug delivery systems involve multiple mechanisms for drug release. To guarantee the absence of dose dumping and the maintenance of the intended rate of in vivo drug release, the USP mandates that the cumulative proportion of from those of traditional dosage formulations. A controlled release dosage form requires a desired drug release profile, while a conventional dosage form must release the majority of the drug from the dosage form in a brief amount of time, as per the USP in vitro dissolution test requirement. In an in vitro dissolution test, for instance, the USP states that at least 80% of the theophylline must be released from a typical capsule within 60 minutes. Nevertheless, particular drug dissolving requirements apply to theophylline extended-release capsules, which can sustain in vivo therapeutic concentrations for a full day. Table 1 displays these specifications (2).

There are numerous varieties of controlled medication delivery systems available to treat various medical disorders. The makeup of the formulation and manufacturing methods has an impact on these systems' in vivo performance. These systems often include a polymer or mixtures of polymers, waxy materials, and other functional excipients in addition to the active component. To accomplish controlled drug release from these systems, numerous strategies and technologies are available. Tablets with controlled release, for instance, may be matrix or depot formulations. One can use either polymer to achieve controlled release of medicines from matrix tablet formulations and/or materials with wax. There are several polymers with different molecular weights that can be utilized to create controlled release medication delivery systems. as well as several grades. It is common knowledge that the molecular weights of these polymers affect the properties of drug release.

The performance of the product may be impacted by variations in the manufacturing techniques used for the various kinds of controlled release medication delivery systems. Granules with the active components could be granulated using wet, hot-melt, fluid-bed, or roller-compaction granulation procedures, for instance, during the production of controlled release matrix tablets.

A controlled release drug delivery system's in vitro or in vivo drug release profile should be taken into account during the development stage, along with other performance characteristics like tablet hardness (for controlled release tablets) or the desired rate of polymer degradation (for implantable or injectable parenteral drug delivery systems).

---

       
           
       
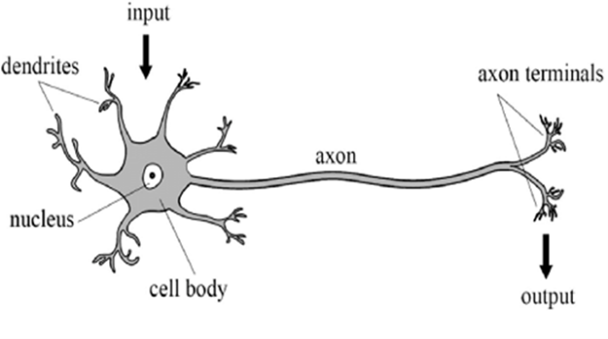
Fig. (1). Conceptual structure of a biological neuron

---

The intricacy of controlled release formulations often makes it difficult to understand the relationship between the formulation and process factors and the previously described performance characteristics of the drug delivery systems under control. As a result, it is frequently challenging to predict a formulation's performance quantitatively using the drug's and the excipients' fundamental physicochemical qualities (3).

It follows that the design and development of these systems is a multivariate optimization process and could be highly difficult given the complexity of the manufacturing processes and composition of the controlled release drug delivery systems stated earlier. A statistical technique called response surface methodology (RSM), which is based on polynomial regression, has been employed in the creation and formulation of various controlled release medication delivery strategies. These drug delivery methods include, for instance, iontophoretic transdermal administration of thyrotropin-releasing hormone, sustained release matrix tablets, and controlled release microcapsules and microspheres. RSM is useful for estimating simple functions or low dimensionality data. This polynomial technique does have certain drawbacks, though. Only under few situations could RSM be useful, as well as a low degree polynomial. First, a suitable response surface model for each response variable must be constructed in order to optimize issues with multiple responses. Next, a collection of independent variables must be found in order to optimize every answer or maintain them within the intended ranges. Because of this, optimizing a multiple response model using the RSM technique may be very difficult. Furthermore, the polynomial equation's coefficient count rapidly grows with the number of input variables. Therefore, the use of RSM for multi-objective optimization, like the creation of controlled release medication delivery systems, would be hampered by the limitations of the polynomial technique (4).

Artificial Neural Network (ANN) is an alternative to the statistical approach for developing controlled release drug delivery systems. The ANN's unique characteristics render the model highly valuable in scenarios where the functional relationship between the inputs and outputs is ambiguous. An ANN model can have a number of the following features:

(1) Multiple independent and dependent variables can be handled simultaneously by an ANN model in a single model (such as a back propagation model).

(2) Since the ANN model is able to learn the latent correlations between the causal factors and response, it is not necessary to know the functional relationship between the independent and dependent variables beforehand (5).

(3) The ANN model, which employs a black box-like methodology, is successful in simulating nonlinear interactions between the independent and dependent variables (6). This is due to the fact that end users do not need to have a thorough understanding of the ANN model's implementation or inner workings.

(4) The ANN model is capable of formulation optimization and prediction, and it is updatable with fresh data. One can utilize the ANN models to forecast the outcome.

In multi-dimensional situations like formulation development, where the ANN models demonstrated superior fitting and prediction abilities over the RSM approach, the efficacy of ANN models in learning the linkages has been demonstrated (7).

A brief overview of artificial neural networks (ANN):

Artificial Neural Networks: What Are They

Artificial neural networks (ANN) are computer programs that use various learning algorithms that are capable of experience-based learning to mimic some functions of the human brain. The amazing information processing characteristics of the human brain, such as high parallelism, robustness, learning, fault and failure tolerance, nonlinearity, and the capacity to handle ambiguous and imprecise input, are shared by artificial neural networks (ANNs). Consequently, complex real-world issues including pattern recognition, clustering, function approximation, and optimization can be resolved with ANN (8).

ANN models come in a wide variety and have been designed for a wide range of uses. Training an ANN model can be either supervised or unsupervised depending on the learning (training) algorithm. In unsupervised training, the ANN model is given input data alone and is trained to identify patterns in the data. In supervised training, input/output data sets are sent to the ANN model. A feedforward or feedback connection between ANNs can exist depending on their topology. Cycles in the connections between nodes do not occur in a feedforward artificial neural network model. There are cycles in the connections of a feedback or recurrent artificial neural network model. Some feedback artificial neural network (ANN) models need the ANN model to iterate at each presentation of an input (9).

Different ANN model types:

According to their functions, ANN models fall into one of three categories :

1.  Joining networks together.

2. Networks that extract features.

3. Networks that are not adaptable.

Associating networks require input (independent variable) and correlated output (dependent variable) values to execute supervised learning. Associating networks are used for data classification and prediction. For unsupervised or competitive learning, feature-extracting networks. which are employed in data dimension reduction only require input values. When nonadaptive networks are given an incomplete data set, they require input values in order to learn the pattern of the inputs and rebuild them. Out of these three ANN model types, associating networks can be used to create controlled release formulations because the relationship between formulation and process factors and the drug release profiles of the controlled release drug delivery systems is not well understood and is nonlinear. It is possible to map the relationship between the formulation and process variables by associating ANN models (10).

Therefore, the purpose of this review is to determine whether associating network models is a valuable tool for designing and developing controlled release drug delivery systems. First presented by Rumelhart et al. the associated ANN relies on delta rule back-propagation of mistakes. Since then, numerous back-propagation-based learning algorithms have been created. The most often used algorithms in ANN for process and composition optimization are these ones (11, 12).

Basic transmission backward Structure of the ANN model:

Replication in reverse, ANN models feature a multi-layered design. There is no computer activity in the first layer, which is referred to as the input layer. It only serves as an input method for the first hidden layer, where independent variables such different important formulation and process elements are sent in. As the output layer, which is the final layer, is used to process the results for the dependent variables, like the outputs (in vitro drug release profiles). hidden levels. remain between the output and input layers and act as the link between the input and cutout layers. It is possible for the connection to be partially or fully connected. Every node in the first layer is connected to every other node in the second layer of a fully connected artificial neural network (ANN). A first layer node does not need to be connected to every second-layer node in partially connected ANN models. There are two possible connection directions: feed forward and bi-directional. The nodes in the first layer transmit their output for a feed forward connection. The problem's complexity dictates how many hidden layers there are. Due to the fact that one hidden layer is typically sufficient to produce an accurate forecast, many ANN models only have one hidden layer. It is possible to simulate complex problems with multiple hidden layers. The structural elements of an ANN are its processing elements, also referred to as artificial nodes or neurons. Using their transfer function, these artificial nodes process data based on weighted inputs and output the results. Weighted linkages connect the nodes in neighbouring layers completely or partially. The weighted outputs from the previous layer added together comprise the net input into the layer node (13, 14). During the learning process of the ANN model, the weight factors of the links between the processing nodes are crucial. The ANN model's memory capacity is comprised of the weight components, whose numerical values vary based on the training data sets. This allows the model to minimize the discrepancy between the expected and actual outputs. Therefore, throughout the learning process, the relationship between the causative elements and the response is mapped.

The output value of the node is calculated using the transfer function of the processing nodes, taking into account the total net input from nodes in the previous layer. As may be seen in the following equation, the sigmoid function is the most commonly employed transfer function.

1. Results obtained from a node

2. The function or categorization that needs to be taught is difficult.

3. the architectural

4. The kind of function that activates hidden nodes

5. A training algorithm

Overfitting or memorizing of the training data set might result from having too many hidden nodes or layers, which would impair the ANN model's capacity to learn. A number of investigators have presented heuristics to choose the number of hidden nodes in an ANN model. According to Kolmogorov's theorem, one hidden node is needed for every arbitrary continuous function to be computed, multiplied by the number of input variables.

Conventionally, heuristic criteria are used to define the number of nodes in the hidden layer. A method that is widely used to determine the ideal number.

In what ways does an ANN model learn:

ANN models are trained to gain experience, which is what they use to learn. Data fitting to a neural network model is a step in the training process. When training an associating ANN model, input/output data sets are given to the model under supervision. When the ANN model is given training data sets (called input/output data sets) or data, it adjusts the weighting factors of the linkages among the processing nodes. This process is known as training or learning. The training data set can be fed to the network model in two different ways: as a whole batch (batch training) or as an example-by-example (called incremental training) After processing each sample in the incremental training process, or after processing the training data as a whole, the weights are changed (15, 16).

---

       
           
       
Fig. (2). A schematic of four-layered artificial network

---

The training data set is given to the model in the feedforward phase. It shows how the processing nodes in the hidden layer combine the inputs depending on the randomly given weight values. It shows how the output is computed using the sigmoid transfer function. At the output layer, the anticipated output or outputs) for this input are available. The output error is estimated initially in the back-propagation step. The process of doing this involves comparing the predicted and actual output numbers. Weight adjustments are then computed for each interconnection after errors for each processing node are determined. The model receives the weight adjustment and is then sent back for a small weight correction need definition in order to train the back-propagation ANN model. The variable known as the learning rate (n) regulates the rate at which knowledge is acquired. ANN model will learn faster with a higher learning rate. On the other hand, an excessively high learning rate may cause the weight change oscillation to surpass a near-optimal weight factor w and hinder the convergence of the error surface. However, the ANN model might encounter a local error minimum rather than the global minimum if the learning rate is too slow. Commencing at a high learning rate and gradually lowering it over time can help to facilitate the learning process. Learning at a steady pace of 0.1–10%.

To prevent local minima and lessen weight change oscillation, the momentum coefficient (u) is employed in the weight updating process for back-propagation ANNs. A smooth effect is achieved by relating the weight change to the preceding weight change in order to achieve faster learning without oscillation. How much of the previous weight change is added to the new weight change is determined by the momentum coefficient. Searching for a set of weight factors for the ANN model in order to minimize prediction errors is known as convergence. The most widely used convergence criterion is based on the sum of squared errors. Oversaw ANN networks calculate the error, or difference, between the expected and actual output values during training.

An increase in the number of hidden nodes or training iterations results in an infinite decrease in training error, such as SSE, for the training data set. Learning is the cause of the SSE's initial rapid decline (17, !8).

subsequent slow reduction of SSE could be attributed to memorization or over-fitting because of the excessively large number of training cycles or excessive number of hidden nodes. On the other hand, the test error decreases initially, but subsequently increases due to memorization and over-fitting of the ANN model. Thus, the training should be stopped when the test error starts to increase, and the optimal number of hidden nodes should be picked when the test error is the minimum.

Functions of the ANN model for prediction and optimization:

If a trained artificial neural network (ANN) is given a set of input values, it may be used to anticipate responses such as drug release patterns. Processing variables and formulation parameters like polymer concentration and medication loading are examples of these inputs. A well-trained artificial neural network (ANN) model's prediction function can provide answers to hypothetical inquiries like, "What kind of drug release profile can we get if we decrease the polymer concentration in the controlled release matrix tablet formulations?" To get a desired formulation, it might be necessary to optimize the formulation and process parameters by examining all potential combinations of the two. This could be a laborious and time-consuming operation. Genetic algorithms (GAS) with trained neural network model integration may be one of the solutions for optimization of such controlled release formulations.

Adaptive heuristic search algorithms, or "survival of the fittest," are the foundation of evolutionary theory of natural selection and constitute genetic algorithms. They offer a clever use of a random search inside a predefined search area to find effective solutions (such formulation compositions) for challenging high-dimensional issues quickly. Based on the generalized distance function method or the desirability function method, the ANN software uses optimization to find solutions that provide the least amount of error between the expected and desired answer. The fitness function, or connection between inputs and outputs, may be found by training neural networks. This information can then be utilized for optimization utilizing genetic algorithms or other search techniques.

Combining ANN with GAs creates a loop-based on the ANN prediction function and the GA exploitation function. When comparing the projected output responses of the ANN with the desired outputs, the new inputs produced by GAs are taken into consideration. This procedure is repeated until the intended output is achieved with optimum or nearly optimal input combinations (optimal formulation or process variables). Thus, this loop offers a strong tool for optimizing the controlled release formalization. For instance, if the ideal or intended drug release profiles are known, an ANN model trained on GA software may be used to extract the ideal formulation and process variables. Recently, standalone software packages containing both the ANN and GA for prediction/optimization applications have been made available by certain commercial computer programmers. CAD/Chem is one instance of a commercially available software suite.

How can I develop controlled release medication delivery systems using artificial neural networks (ANN) and other similar techniques:

Starting with a desired in vivo plasma concentration profile, controlled release drug delivery devices are designed. Developing and refining a controlled release formulation only via study might be expensive and impractical. If a level A in vitro/in vivo correlation (IVIVC) is present, in vitro release studies might take the place of in vivo drug release investigations. But for many controlled release formulations, poor IVIVC is a regular occurrence. An ANN might be used to create IVIVC. If there is any connection between the in vitro Once in vitro release properties are known, the job of creating a controlled release formulation would be to determine the relationship between the formulation factors (or process variables) and in vitro release properties. A latent link between the response (in vitro release characteristics) and the causative causes (formulation variables) may be learned using an ANN model. Deconvoluting the appropriate in vivo plasma concentration profiles yields the in vivo absorption pro files, which can then be linked with the in vitro release profiles (19).

The technique of obtaining the in vivo absorption profile of a dosage form provided based on the drug's pharmacokinetic properties using mathematical methods is known as deconvolution of a plasma concentration profile. The Wagner-Nelson approach for a one compartmental model, the Loo-Riegelman method for a two compartmental model, or a model agnostic computer software like PCDCON may all be used to deconstruct the target or ideal in vivo release profile.

When developing formulations, it is common to compare two dissolving profiles. When the similarity factor is between 50 and 100 and the difference factor (f) is between 0 and 15, the US Food and Drug Administration considers two dissolving profiles to be comparable. The following two equations determine the difference factor (f) and the similarity factor (f), respectively.

Gathering information to train the ANN model:

For any trained ANN model to produce accurate results, data are the most crucial component as the data that these models are exposed to is used to train them. Information sent into the ANN software in pairs as a cause-and-effect connection for back-propagation ANNs and other associated networks. The data must be interpolated using ANN models as they are required to generalize for unknown situations (data not supplied during the training process). A trained artificial neural network (ANN) model's prediction capacity is typically measured within the input/output data space limit that the model is given during training. It may be criticized to extrapolate outside of this data space. As a result, the training dataset should have enough size to include all potential known variations in the issue area. In general, stronger and more dependable prediction and optimization outcomes come from a solid data set that investigates Since employing an experimental design guarantees the independence among the formulation components, statistical experimental designs model formulations to minimize the number of trials for data gathering. Subsequently, information may be gathered from tests conducted using the DOE. Obtaining trustworthy data to train the ANN model, carefully regulated experimental conditions are required (20).
The following are some instances of formulation optimization using DOE in conjunction with ANN. Takayama et al. used a two-factor spherical second-order composite experimental design to create model formulations for transdermal medication delivery devices. Takayama et al. created model formulations for prolonged release matrix tablets using a three-factor, two-level composite experimental approach. Hussain et al. designed model-controlled release matrix tablet formulations of chlorpheniramine maleate using a four-component simplex centroid mixture design. Vaithiyalingam et al. used a three-factor, three-level central composite face-cantered design to create model-controlled bead formulations.

Development of ANN models for optimization and prediction:

Creation of models:

In order to construct an ANN model, the architecture must first be determined. This includes defining the number of nodes in the input and output layers, the number of hidden layers, and the number of hidden nodes. The problem to be researched determines the number of inputs and outputs. There should be as few inputs as possible. adding additional factors may skew the results and cause confusion. How many hidden nodes should be used is the most crucial question in the construction of the ANN model. The number of hidden nodes cannot be determined by a magic formula, as was stated in the section on ANN basic architecture. There are just a few guidelines for Determining the smooth factor, learning rate, and kind of transfer function may also be necessary when building an ANN model. While some software programs allow the end user to pick some of these parameters for modelling, others may already specify some of these aspects and leave it up to the user to establish the ANN architecture. The ANN model architecture arc development examples for controlled release formulation optimization are as follows (21). An ANN model was created. the work of Hussain et al. Four formulation variables corresponded to four inputs in the ANN model. These variables included the concentrations of polymers like carboxymethylcellulose (CMC), hydroxypropyl cellulose (HPC), hydroxyethyl cellulose (HBC), and hydroxypropyl methylcellulose (HPMC). Two outputs, release exponent (N) and the amount of time needed for 50% of the drug to be released, corresponded to the two response variables. There were 4, 6, 8, 10, 12, and 14 hidden nodes that were used in the different training models. Since the training set's residual sum of squared errors was found to be the lowest, eight hidden nodes were selected for the trained model's hidden layer. The moment factor and scarming rate, respectively. 0.9 and 0.25.

Training of ANN model:

An ANN model was created by Hussain et al. in a different study place for experimentation. This means that a wide range of data from various experimental settings, such as varied formulation composition and process parameters, must be included in the training data set, which must be reasonably big to contain all the necessary information.

The test data set is a separate collection of data that the back propagation algorithm saves for later use rather than using it for training. It is used to monitor the ANN model's training progress and is sent to it on a regular basis. Put differently, serves as a third-party monitor for the algorithm's development. The training and the exam both first decline, as was previously described. However, it indicates that the ANN model is beginning to overfit the data when the test energy starts to decline or when it naturally begins to rise. At this point, the training needs to be stopped. Reducing the number of hidden layers and units is typically advised when over-learning occurs during the training phase. The purpose of the validation set is to confirm that the input-output connection found in the training and test sets is genuine and not the result of process artifacts. Data that fall within the training data set's bounds but are not included in the other data sets should be included in the validation data. Before the final model is trained for deployment, it is verified for correctness using the validation data set (22,23).

The quantity of data needed in each set to train the ANN models is not determined by any mathematical formula. To separate the gathered data into training, test, and validation sets, there are only a few general guidelines available. Baum et al. suggested that the training subset should be at least equal to the product of the inverse of the minimal goal error and the number of weights in the models. It is recommended by Dowla et al. that the ratio of the training subset sample to the number of weight components be more than 10.

ANN applications in the development of medicine delivery systems with controlled release:
Though still small, ANN is being more and more used in the design of controlled release medication delivery systems. Applications of artificial neural networks (ANN) have been used in the development of controlled release formulations, including formulation and manufacturing process optimization. Most of these applications have been concentrated on medication delivery systems with controlled release for oral usage (24,25). 

Preformulation
In order to create oral controlled release dosage forms, ANN models have been employed during the preformulation phase. Ebube et al. developed an ANN model to forecast the physicochemical features of hydrophilic polymers and blends of hydrophilic polymers, which are frequently utilized to manufacture controlled released the relationships between the composition of polymer blends and the viscosity of polymer solutions; the positions of the blend and the water uptake profiles; and the relationships between the moisture contents of the polymers and their glass transition temperatures were all learned by the trained artificial neural network (ANN) model, which was constructed using CAD/Chem software (version 5.0). The study's findings showed that the ANN model accurately predicted, with a low prediction error of 0-8%, the viscosities, glass transition temperatures, and water absorption of several hydrophilic polymers and their physical blends. In order to create sustained release formulations that necessitate the use of a quick hydrating polymer matrix, a trained artificial neural network (ANN) model can be helpful in gathering information during the preformulation step (26,27).

Forecasting and Enhancement of Controlled Release Drug Administration Methods:
To anticipate and optimize various kinds of controlled release formulations, researchers have employed several ANN models and learning algorithms (28).

Tablets with regulated release:

Chen and colleagues employed pharmacokinetic and artificial neural network (ANN) simulations for the design of controlled-release formulations. The 22 tablet formulations of a model sympathomimetic medication were utilized as the inputs for the ANN model, together with seven formulation variables and three additional tablet variables (moisture, particle size, and hardness). The results were the cumulative in vitro percentage of medication released at ten distinct sampling times. CAD/Chem software (version 4.6) was used to design and train the ANN model utilizing the input and output data sets. The ANN model after training the similarity coefficient f (29).

 An ANN model was created by Zupan?i? Boži? et al. to improve the use of diclofenac sodium sustained release tablets The concentrations of ceryl alcohol, polyvinylpyrrolidone K-30, and magnesium Meurate, as well as the duration of the sample, were selected as formulation factors (30). The hidden layer had twelve hidden nodes. The output was the proportion of drug released at each sample time point. To forecast release profile and improve formulation composition depending on the proportion of drug released, a trained artificial neural network (ANN) model was utilized. An ANN model was utilized in Takayama et al.'s simultaneous optimization approach to optimize controlled release theophylline tablets made using Controse, a combination of lactose, cornstarch, and hydroxy propyl methyl cellulose. The anticipated release parameters came from the Peppas equation, namely (release order) and log & release constant. a collection of causative variables and release parameters for training The GRNN model that was developed was employed to forecast the formulation and process variables for the optimized formulations. This might result in the intended in vitro drug release profiles. Then, two improved formulations were made and put through an in vitro evaluation. A comparison of the in vitro profiles observed and predicted by GRNN and my computed coefficients showed no difference between the experimental and anticipated profiles. Based on the similarity factor, f, and difference factor, observed drug release patterns for the two tested formulations.
To maximize salbutamol sulphate osmotic absorption, a formulation optimization algorithm built on the ANN model was created. utilized as inputs, and the output was determined by calculating the proportion of medication released at every sample point. The ANN models were trained using the leave-one-out cross-validation method. Based on the forecast of every point, a comprehensive release profile was acquired. The similarity factor f2, f, was used to calculate the degree of similarity between the dissolution profile that the ANN predicted and the real one. High scores above 60 indicate that the dissolution patterns predicted by the ANN were Comparable to the dissolution profiles seen in the actual testing. The impact of process and formulation factors, including weight gain, curing time, and plasticizer concentration, on the in vitro release profile of verapamil HCI from multi-particulate beads formulated with a new aqueous based pseudo latex was studied by Vaithiyalingam et al. using the an ANN model (31,32).

Microspheres, beads and pellets - particulates with controlled release:

Peh et al. created many artificial neural network (ANN) models to forecast the dissolution profiles of matrix-controlled release theophylline pellets made using glyceryl monostearate (GMS) and microcrystalline cellulose (MCC). The Neural software was used to construct the multi-layered perceptron (MLP) neural network, which has four inputs and one output. For the purpose of training the ANN model, the conjugate gradient and simulated annealing techniques were employed. The amounts of GMS and MCC in the formulations, the sampling period, and the variation in release rates between the two previous time points were as inputs, and the output, or proportion of medication released at each sample point, was calculated. To train the ANN models, the leave-one-out cross-validation method was employed. Based on the estimation of every time point, a comprehensive release profile was acquired. Using the similarity factor, f., the degree of similarity between the dissolution profile that the ANN predicted and the real one was ascertained. High values (above 60) in the ANN projected dissolution profiles showed that they were similar to the dissolution profiles from the physical testing (33,34).
Using artificial neural networks (ANNs), Vaithiyalingam et al. modelled the impact of process and formulation factors, such as weight increase, curing time, and plasticizer concentration, on the in vitro release profile of verapamil HCI from multi-particulate beads formed with model.

To verify that the trained ANN model could predict and generalize, four further formulations were created and assessed. The findings indicated that the analysis of process and formulation parameters may be accomplished with flexibility and accuracy using the ANN approach.

Formulation Trans dermally:

Takayama et al. designed an artificial neural network (ANN) to improve a transdermal ketoprofen hydrogel containing O-ethyl menthol (MET) as percutaneous absorption on enhancer. For optimization, the generalized distance function approach was used. The ethanol and MET contents were chosen. The essential irritation score, lag time, and penetration rate (R). We choose to use them as response factors. The ANN model was trained using a collection of data that included response variables and causative components. The gel composition was optimized by calculating the best values of each response variable. After that, the ideal Formulation was created and assessed. The observed outcomes for each of the optimal formulation's answers matched each other rather well (35).

 

ANNs Limitations:

The mechanical nature of the link seen between the variables cannot be explained by ANN models. A formulator may require a large amount of training data and computer time in order to produce a trustworthy and trained ANN model. The first stages of work, such designing experiments and gathering data, could take longer than the conventional method employed by skilled formulation scientists (36). Furthermore, it's critical for formulators to understand that no one piece of software or modelling technique is capable of solving every issue.

CONCLUSION:
Two different methods can be used to create and produce controlled die compositions. Understanding the impact of the formulation and process parameters is one strategy. effectiveness of the formulations with controlled release. The alternative strategy is to create the formulation using ANN and traditional modelling techniques, such statistics. The first method helps a formulator comprehend how process parameters and formulation ingredients impact controlled release medication delivery systems. But in the end, this method takes longer for a formulator to design and create an ideal controlled release medication delivery system. However, the second method simplifies the formulation optimization process by utilizing suitable conventional and artificial neural network models to optimize a controlled release drug delivery system. Furthermore, this methodology may also be utilized for the basic research about the impact of formulation and process factors on the delivery system.

Conflict of Interest: Authors declare no conflict of interest.

Bottom of Form

REFERENCE

1. D.C. Montgomery, Response surface methods and other approaches to process optimization, in: Design and Analysis of Experiments, Wiley, New York, 2001, pp. 427-500
2. A.S. Hussain, X.Q. Yu, R.D. Johnson, Application of neural computing in pharmaceutical product development, Pharm.Res. 8 (1991) 1248-1252.
3. A. Boza, Y. De la Cruz, G. Jordan, U. Jauregui-Haza, A. Aleman, I. Caraballo, Statistical optimization of a sustained- release matrix tablet of libenzapril disodium, Drug Dev. Ind. Pharm. 26 (2000) 1303-1307.
4. M. Farivar, H.S. Kas, L. Oner, A.A. Hincal, Factorial design- based optimization of the formulation of isosorbide-5-mono-nitrate microcapsules, J. Microencapsule. 10 (1993) 309-317.
5. K. Abu-Izza, L. Garcia-Contreras, D.R. Lu, Preparation and evaluation of zidovudine-loaded sustained-release micro- spheres. 2. Optimization of multiple response variables, J. Pharm. Sci. 85 (1996) 572-576.
6. Y.Y. Huang, S.M. Wu, C.Y. Wang, Response surface method: a novel strategy to optimize iontophoretic transdermal delivery of thyrotropin-releasing hormone, Pharm. Res. 13 (1996) 547-552.
7. J. Fu, Y. K. Jan, and M. Jones, "Development of intelligent model to determine favorable wheelchair tilt and recline angles for people with spinal cord injury," Conference proceedings : Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference., vol. 2011, 2011 pp. 2045-8.
8. J. Yang, H. Singh, E. L. Hines, F. Schlaghecken, D. D. Iliescu, M. S. Leeson, and N. G. Stocks, "Channel selection and classification of electroencephalogram signals: an artificial neural network and genetic algorithm-based approach," Artif. Intell. Med., vol. 55, June 2012.  pp. 117-26.
9. F. Bettella, D. Rasinski, and E. W. Knapp, "Protein secondary structure prediction with SPARROW," J. Chem. Inform. Model., vol. 52, Feb. 2012 pp. 545-56.
10. B. Liu and Y. Jiang, "A multitarget training method for artificial neural network with application to computer-aided diagnosis," Med. Phys., vol. 40,  Jan 2013. p. 011908.
11. W. Zhao and C. E. Davis, "A modified artificial immune system based pattern recognition approach an application to clinical diagnostics," Artif. Intell. Med., vol. 52, May 2011. pp. 1-9.
12. Ali, A. H. Neural network principal component using adaptive principal component extractor (APEX). IEEE Int. Symp. on CIMS 2003 101–104.
13. Amiri, M., H. Davande, A. Sadeghian, and S. A. Seyyedsalehi.  Auto-associative neural network based on new hybrid model of SFNN and GRNN. In: International Joint Conference on Neural Networks, 2007. 2664–2670.
14. Brier, E., J. M. Zurada, and G. R. Aronoff.  Neural network predicted peak and trough of gentamicin concentrations. Pharm. Res.1995. 12:406–412.
15. Chen, T., and H. Chen. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical system. IEEE Trans. Neural Networks 1995 6:911–917.
16. Ghaffari A., H. Abdollahi, M. R. Khoshayand, I. Soltani Bozchalooi, A. Dadgar, and M. Rafiee-Tehrani. Performance comparison of neural network training algorithms in modelling of bimodal drug delivery. Int. J. Pharm. 2006. 327:126–138.
17. Hossieni, S. M., M. Amiri, S. Najarian, and J. Dargahi. Application of artificial neural networks for estimation of tumour characteristics in biological tissue. Int. J. Med. Rob. Comp. Assoc. Surg. 2007. 3:235–244.
18. Snee, R.D. Quality by design-four years and three myths later. Pharm. Proc. 2009, 2, 14-
19. Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modelling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727.
20. V.P. Shah, Dissolution testing of immediate-release solid oral dosage forms, in: G.L. Amidon, J.R. Robinson, R.L. Williams (Eds.), Scientific Foundation for Regulating Drug Product Quality, AAPS Press, Alexandria, VA, 1997, pp. 205-212.
21. K. Takayama, J. Takahara, M. Fujikawa, H. Ichikawa, T. Nagai, Formula optimization based on artificial neural networks in transdermal drug delivery, J. Control. Release 62 (1999) 161-170.
22. S. Vaithiyalingam, M.A. Khan, Optimization and characterization of controlled release multi-particulate beads formulated with a customized cellulose acetate butyrate dispersion, Int. J. Pharm. 234 (2002) 179-193.
23. A.S. Hussain, P. Shivanand, R.D. Johnson, Application of neural computing in pharmaceutical product development: computer aided formulation design, Drug Dev. Ind. Pharm. 20 (1994) 1739-1752.
24. F.U. Dowla, L.L.. Rogers, in: Solving Problems in Environmental Engineering and Geosciences With Artificial Neural Networks, MIT Press, Cambridge, MA, 1995.
25. C.G. Looney, Advances in feedforward neural networks: demystifying knowledge acquiring black boxes, IEEE Trans. Knowledge Data Eng. 8 (1996) 211-226.
26. D. Zupancic Bozic, F. Vrecer, F. Kozjek, Optimization of diclofenac sodium dissolution from sustained release formulations using an artificial neural network, Eur. J. Pharm. Sci. 5 (1997) 163-169.
27. K. Takayama, A. Morva, M. Fujikawa, Y. Hattori, Y. Obata, T. Nagai, Formula optimization of theophylline controlled- release tablet based on artificial neural networks, J. Control. Release 68 (2000) 175-186.
28. R. Sabet, A. Fassihi, B. Hemmateenejad, L. Saghaei, R. Miri, and M. Gholami, "Computer-aided design of novel antibacterial 3- hydroxypyridine-4-ones: application of QSAR methods based on the MOLMAP approach," J. Computer. Aid. Mol. Des., vol. 26, March 2012, pp. 349-61.
29. M. Koba, "Application of artificial neural networks for the prediction of antitumor activity of a series of acridine derivatives," Med. Chem., vol. 8, May 2012. pp. 309-19.
30. B. B. Andreas Breindl, Timothy Clark, Robert C. Glen, "Prediction of the n-Octanol/water partition coefficient, log p, using a combination of semiempirical calculations and a neural network," J. Mol. Model., vol. 3, 1997, pp. 142-155.
31. D. Eros, I. Kovesdi, L. Orfi, K. Takacs-Novak, G. Acsady, and G. Keri, "Reliability of log P predictions based on calculated molecular descriptors: a critical review," Curr. Med. Chem., vol. 9, Oct 2002. pp. 1819- 29.
32. A. J. Wilczynska Piliszek, S. Piliszek, and J. Falandysz, "Use of quantitative-structure property relationship (QSPR) and artificial neural network (ANN) based approaches for estimating the octanol-water partition coefficients of the 209 chlorinated trans- azobenzene congeners," J. Environ. Sci. Health, B., vol. 47, 2012. pp. 111-28.
33. A. Yan, X. Chen, R. Zhang, M. Liu, Z. Hu, and B. T. Fan, "Predicting the standard enthalpy (deltaH0f) and entropy (SO) of alkanes by artificial neural networks," SAR. OSAR. Environ. Res., vol. 11, 2000. pp. 235-44.
34. S. Liu, "Neural Network-Topological Indices Approach to the Prediction of Properties of Alkene," J. Chem. Inform. Computer Sci., vol. 37, 1997. pp. 1146.
35. E. S. Goll and P. C. Jurs, "Prediction of Vapor Pressures of Hydrocarbons and Halo hydrocarbons from Molecular Structure with a Computational Neural Network Model," J. Chem. Inform. Computer Sci. Vol. 40, May 2000. Pp. 859-879
36. S. Piliszek, A. J. Wilczynska-Piliszek, and J. Falandysz, "Prediction of subcooled vapor pressures (log PL) of 399 polychlorinated trans azoxybenzenes by using the QSPR and ANN, Computer. Sci., vol. 39, 1999. pp. 1081-1089.