Abstract
In the pharmaceutical business, ultraviolet (UV) spectroscopy has been an essential analytical instrument for more than 35 years. The low cost and low maintenance needs of this approach make it highly prized, particularly by small-scale companies. In ultraviolet spectroscopy, monochrome absorption of light by colourless materials in the near-ultraviolet spectrum of the spectrum that is, between 200 and 400 nm is measured. Identification, potency, purity, and quality assessment of different chemicals are all part of the analysis processes and are crucial to pharmaceutical analysis. During the production of drugs, this includes inspecting the raw materials and intermediates. Dissociation constants are a crucial component in the creation and refinement of novel medicinal molecules. Effective formulation development depends on the ability to obtain the absorbance spectra of chemicals, whether they are in solution or solid form, which is made possible by UV-visible spectroscopy. In pharmaceutical analysis, this procedure is essential for ascertaining the identity, potency, calibre, as well as the compound's purity. It also covers the analysis of intermediate and raw materials used in the manufacturing of pharmaceuticals. The practical and quantitative features of UV spectroscopy are described in this study.
Keywords
UV Spectroscopy, Identity, Strength, Quality, Purity, Drug Manufacturing, Qualitative, Quantitative
Introduction
In this study, This investigation assessed molecule absorption at wavelengths ranging from 190 to 800 nm, encompassing the visible (400-800 nm) and ultraviolet (190-400 nm) portions of the electromagnetic spectrum. UV spectroscopy is the name given to optical techniques that make use of the visible, ultraviolet, and near-infrared spectrums. A homogeneous solution's thickness (b) and concentration (c) have an impact on a cell's capacity to absorb monochromatic light. I-stands for both the electrical event's severity and the power transfer.
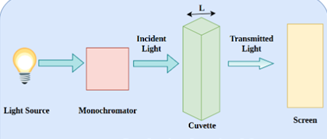
Figure 1 Mechanism of absorption
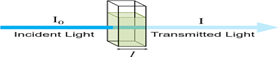
One way to figure out how much radiation a material has absorbed is to measure its transmittance. It is expressed as \( T = \frac{I}{I_0} \) and is The definition of it is the proportion of input power (I) to input power. (I?). The formula for calculating the percentage transmittance (%T) is ( %T = 100 \times T \). After that, absorbance (A) is calculated using the following formula: \( A = 2-\log_{10}(%T) \). A material that has a transmittance percentage of 100% does not absorb any light. On the other hand, transmittance is 0%, indicating infinite absorption, if all light is absorbed.
Relative to quality control and routine analysis, spectrophotometric techniques like derivative and ratio spectra spectrophotometry are frequently used in research or industrial laboratories. These techniques are better than hyphenated analytical methods such as GC-MS, LC-NMR, and LC-MS, the usually need for preparatory steps like extraction and other laborious procedures. These methods' intricate parts also add to their increased expenses and extended analysis durations. Analytical chemists place a great deal of emphasis on the quantitative spectrophotometric resolution of mixtures with overlapping spectra because of these factors. When evaluating mixtures, spectrophotometric methods are valued for their ease of use, rapidity, sensitivity, and affordability. New analytical approaches or procedures are needed to resolve complicated mixtures with accuracy, precision, and reliability.
These approaches frequently entail mathematics or a blend of traditional and modern techniques. Analysts are able to select the most appropriate spectrophotometric approach based on a wide variety of options. Absorption spectroscopy is especially helpful and frequently used for quantitative analysis since the amount of analyte and the amount of light absorbed are closely connected. The simplicity, speed, accuracy, precision, and efficiency of this approach make it the preferred one. When there is overlap in the chemical spectra, spectrophotometric multicomponent analysis can be applied. The concentration of each component can be determined using the equation when the spectra overlap, provided that they are not identical. Even in cases of significant spectral overlap, this approach performs well in chemical analysis. All spectrophotometric methods for examining materials with several components are based on a few fundamental ideas that hold true at all wavelengths:
1. Additivity of Absorbance: A solution's absorbance is the proportion of each component's absorption. If each material is tested separately under the identical circumstances, they all show equal light absorption at any wavelength. By looking at the meter's spectrum combination is the sum of the spectra of each of its constituent parts, this idea was empirically verified. Consequently, the spectrum of the second component can be obtained by deducting the spectrum of the first component from the total absorbance.
2. Measured Absorbance: The difference between the sample cell's total absorbance and the reference (blank) cell's absorbance is the absorbance that is measured.
3. The Law of Beer-Lambert:
In accordance with the Beer-Lambert Law (\(A = abc\)), at a path length of one, the absorbance must likewise be zero (\(A = 0\)) when the concentration is zero (\(c = 0\)). This suggests that the best course for the calibration line should go via the origin. In actuality, the calibration plot ought to be near the origin, with a modest intercept value, although it might not cross it exactly. Since the Beer-Lambert Law is only strictly relevant to diluted solutions, applying it at incorrect concentrations can be a significant source of inaccuracy. As the concentration of the solution rises, its accuracy decreases. An unknown solution's absorbance can be measured at the same wavelength as the calibration curve, and its concentration can be inferred from the graph or computed from the slope.
The Beer-Lambert law forms the foundation of UV-visible light spectroscopy. According to this law, the concentration of the absorbing substance (C) and the length of light emitted by the solution (b) are directly proportional to the absorbance of the substance in solution (A). The concentration of absorbed water in the solution can be ascertained using this rule for long-term stability.
The relationship is given by the equation:
The capacity to absorb A is equal to cell length x concentration x molar absorptivity constant.
A = ABC C is equal to A/a b.
where absorbance (A)
Molar absorptivity is a= a.
Path length is b.
C stands for concentration.
By Calculating the absorbance of a solution, this principle enables the quantitative assessment of the concentration of absorbing species in that solution. Adjuvants or coloured complex products can be subjected to spectrophotometric determination for single-component analysis. Nevertheless, multi-component mixture analysis is not a good fit for these techniques. Techniques are categorised as solving either moderately overlapped spectra or severely overlapped spectra, depending on the degree of spectral overlap. The way that different spectroscopic techniques are used to different spectra determines which categories they fall under for multi-component analysis.
- The Electronic Shift or Transition
A molecule or an ion will absorb light in the visible or ultraviolet spectrum when an electrical charge changes its electron makeup. As a result, the electronic state of the molecules in the sample changes when it absorbs light at certain wavelengths. Light energy raises electrons from their ground orbital state to an excited orbital state, also known as an antibonding orbital.
There could be three kinds of ground state orbitals involved:
1. (sigma) (sigma) molecular orbital bonding
2. (pi) (pi) molecular orbital bonding
3. (n) Atomic orbital (non-bonding)
Two other kinds of anti-bonding orbitals could also play a role in the transition:
1. orbital of (sigma*) (sigma star)
2. orbital of (pi*) (pi star)
Since (n) electrons do not take part in bonding, there is no (n*) anti-bonding orbital.
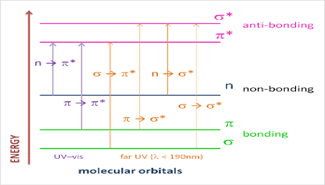
Figure 2:The Electronic transition of the ?, ? and n electrons.
• ? to ? Transition:
During this transition, an electron in a ? bonding orbital is stimulated to the corresponding ?* antibonding orbital. It takes a considerable amount of energy to do this. Methane, for instance, exhibits an absorbance maximum at 125 nm and goes through ? to ?* transitions despite just having C-H bonds. Typically, UV-Vis spectra (200-700 nm) do not show such transitions.
• n to ?* Transition:
When atoms in saturated compounds contain two electrons or nonbonding electrons, this happens. These transitions require less energy than the ? to ?* transitions and can be triggered by light with wavelengths between 150 and 250 nm.
- n to ? and ? to ? Transitions:
Most organic compounds require the transition of n or ? electrons to the ?* excited state in order to have absorption spectra. The absorption peaks are in the spectrally accessible experimental range (200-700 nm), which makes these modifications significant. The molecule's pi electrons have to originate from unsaturated groups. The n to 8* transition has a molar absorbance of 10 to 100 L mol·cm·cm, while the 8 to ?* transition has a molar absorbance of 1000 to 10,000 L mol·cm·cm. These alterations can be brought on by light with wavelengths between 200 and 700 nm.
Recent Development in Ultraviolet Spectroscopy
1] Dual wavelength induction technique
Utilizing this novel technique, binary mixes of chemicals X and Y can be identified if their zero-order absorption spectra overlap between two wavelengths, ?1 and ?2. This technique manages the data pertaining to the difference between various angles (?A - 0), whereas the double wavelength approach necessitates the equilibrium of the disparity between these lines. To lessen the impact of the Y product on ?1 and ?2, the equation (FY) of pure Y of wavelengths was computed using this technique. Determining the concentration X can thus be done by creating a regression equation by graphing the zero-order spectrum of the product concentration X against the concentrations of the absorbance difference (?A).
2] The technology of dual wavelength resolution (DWRT)
With entirely overlapped zero-order absorption spectra, substances X and Y in a binary combination are the subject of analysis using this innovative resolution technique. In these circumstances:
The concentration of component X is exactly related to the absorbance difference ?A (A1 - FY * A2) in the mixture spectrum between two chosen wavelengths (?max of X and ?2)
Since X and component Y completely overlap, the absorbance difference for Y is naturally equal to zero.
Dual wavelength resolution technology (DWRT) is a method for resolving overlapping spectra by employing dual wavelength spectrophotometric techniques, such as induced dual wavelength methods or traditional dual wavelength methods . While these methods are especially helpful in figuring out the concentration of the primary component (X), they do not directly applicable to the secondary component (Y).
To determine the concentration of X:
To find the concentration of the X relation, measure X using either the regular double wavelength approach (where FY = 1) or the induced double wavelength method (where FY ? 1).
To obtain the zero-order absorption spectrum of component X in the mixture:
Divide the computed X concentration by X's normalised spectrum. The entire range of X is divided by the corresponding concentration to yield the normalised spectrum of X, which is a spectrum that depicts the absorptivity of X (axe) at all observed wavelengths.
To obtain the zero-order absorption spectrum of component Y:
The mixture's (X + Y) spectrum is subtracted from the resultant X spectrum. This leads to a division of the Y equation or the D° spectrum of Y. To determine Y's concentration in the mixture, use this equation. The method solves spectral overlap issues and predicts X and Y concentrations accurately in binary mixtures with all overlapping spectra by using the dual wavelength methodology and spectral manipulations.
3] Corrective absorbance technique
The examination of binary mixes with overlapping attributes between components X and Y is described by this method. The absorption coefficient (Abs of ?1 / Abs of ?2) is used to get the average composition Y value. Because X doesn't contribute, the mixture's absorption at ?2 (X + Y) equals the wavelength absorption of pure Y, hence the absorption may be computed using.:
Abs of X at ?1 = Abs ?1 (X+Y)- abs1/abs2 × Abs ?2 (X+Y)
where Abs1 and Abs2 are the combined absorbances of ?1 and ?2 of (X + Y), respectively, and abs1 / abs2 is the absorption coefficient of pure Y (Abs of ?1 / Abs of ?2). The regression equation can be determined by graphing the zero-order spectra of ?1 and ?2 versus the concentration of the absorption value. This will be utilized to ascertain X and Y's range.
- Techniques utilizing absorptivity points
1. Subtraction of absorbance (AS)
The Greek terms "isos" (equal) and "absorptive" (absorptivity) are the source of the name of this novel approach, which is called the isoabsorption point spectrophotometric technique. It means equal absorptivity. It's used to determine components in binary or ternary mixes simultaneously. The combination of medications exhibits equal absorptivity values at the isoabsorption point, behaving as a single component. The concentration of each component in the combination can be found by any complementary approach, however the overall concentration of components X and Y can be computed by measuring the absorbance at this particular point (?iso).
There are conceptual similarities between the absorbance method and the absorbance subtraction (AS) method. When the overlapping spectra of mixtures X and Y cross at the isoabsorption point where the spectrum of Y lies for the spectrum of X, it can be used to identify mixtures where X does not contribute at a particular time (?2). X and Y in the mixture (X + Y) can be estimated using this method using the isoabsorption point, (?iso). One of the elements that have been determined mathematically can be used to determine this. It is possible to independently determine the equivalent absorbance values for X and Y using a few easy methods. Consequently, every element's concentration may be found using the isoabsorption point regression equation alone—no other techniques are required. The concentration of each element X and Y can be found using the isoabsorption point combined regression equation.
2. enhanced absorbance subtraction
This innovative technique can be applied to binary combinations of X and Y when their spectra overlap and the zero spectrum has an isoabsorption point (?iso). Two wavelengths are selected: one X component is the isoabsorption point (?iso), and one Y component exhibits the same absorption at both wavelengths (?2). The product X concentration is directly proportional to the absorbance difference ?A (Aiso - A2) between the two chosen wavelengths when combined. Product Y's absorbance difference is always zero. When the curve generated for pure X is measured, the relationship between (Aiso ? A2) and Aiso is displayed, yielding the following equation:
(Aiso–A2) = b?A Aiso+I?A
where (Aiso ? A2) is the difference between two chosen wavelengths of the pure X spectrum, b?A is the slope, I?A is the intercept, and Aiso is the absorbance of ?iso of X. A's absorbance and Aiso's absorbance are equal. Subtracting the predicted absorbance of X in Aiso from the absorbance recorded in Aiso [ARecorded] yields the absorbance corresponding to Y.
ARecorded = AX+AY
Then, the unified regression equation can be used to determine the concentration of X (CX) or Y (CY). Plotting the zero-order absorbance values (Aiso) against the appropriate concentrations of X or Y yields this equation.
3] Spectrophotometric absorption factor method (a-Factor method)
When examining binary mixtures, a novel spectrophotometric technique called absorption coefficient was applied [18]. When there is a substantial difference in the substance's absorption, the concentration of two elements in a binary mixture should be determined using a straightforward numerical equation to prevent the development of isosorptive elements. In these situations, it is not possible to concurrently separate all medications from other compounds using the isosorption point approach.
The ratio of two absorbances at the intersection (axis, aY) when the absorbance values are equal is known as the absorbance factor, or ?F. The absorption coefficient estimate serves as the foundation for this approach. To determine the concentration of the compound represented as (FCX + CY), a regression equation illustrating the link between Y's absorbance and its corresponding point at the absorbance coefficient can be employed. Therefore, the X concentration can be computed by subtracting the Y concentration, dividing by the total of F, and repeating if the Y concentration is measured separately using a different technique (such as direct spectrophotometry, derivative spectrophotometry, or derivative ratio). In that very moment.
- Techniques employing the area under the curve (AUC)
1] Area under the curve correction method. [ AUC-CM]
A novel technique that is based on the spectrophotometric approach is area under the curve (AUC). It offers a straightforward technique for figuring out how much of an interesting component is present in a binary mixture by looking at its absorption spectral area. This method's primary benefit is its capacity to resolve mixes with significant overlaps. Area under the curve (AUC) data are used to reflect the concentration of the element of interest, and the corrected area under the curve (AUC) shows this. Even at low concentrations, the AUC value exceeds the absorbance value, increasing sensitivity. Using this method to calculate the AUC of each X and Y (where Y extends to X) eliminates the need for Cramer's rule.
2] The method of compensated area under curve (CAUC)
The area under the curve (AUC) is used in place of the derivative spectrum's amplitude in the latest iteration of the derivative compensation method. When two components, X and Y, have absorption spectra that overlap in a vacuum or when minor components (X) are detected alongside major components (Y), it is especially crucial. The AUC a range / AUC b range represents the component (Y)'s AUC in relation to the blank. Measure the absorbance difference of [Mixture (m) – Reference (r)], where m = Ax + Ay and r = Ax, after a mixture containing X and Y is introduced in the sample cell. Record the AUC.
The amount of pure substance (X) in the combination added to the reference material Cx both above and below the required concentration is used to achieve this. The difference spectrum's AUC ratio (AUCa/AUCb) was computed and contrasted with the pure Y AUC ratio that had previously been established. AUCa/AUCb, the AUC ratio of the difference spectrum, was computed and contrasted with the pure Y AUC ratio that was previously established. The compound's AUC will match the AUC of pure Y in the equilibrium state where Cx in the compound equals Cx in the reference pool. The unit of reference is a thinly curved line. The concentration at which the AUC ratio of the mixture of pure component (Y) that was previously present in the spectrum of pure Y at different concentrations can be interpreted as the concentration (Cx) of the image. To find the concentration (Cx), compute the geometric method's regression equation and replace it with the pure Y mean AUC ratio.
4] Subtraction of spectrum
It is advised to use derivative spectrophotometry to improve the resolution of overlapping spectra. The selection of a wavelength at which the signal of one compound is present but that of another is negligible makes determining the existence of a substance all the more crucial. This approach has been effective in the identification of several medications and compounds, as well as individual medications and their fragments.
Unfortunately, the outcomes of some medication combinations are not always visible in direct drug testing that use derivatization techniques of first, second, third, and fourth order absorption spectra or comparison spectra. In order to reduce noise, this problem necessitates developing solutions that involve mathematical transformation of derived spectra with the lowest degree of derivatization. Notwithstanding these issues, derivative spectrophotometry adheres to the fundamentals of classical spectrophotometry, including accurate summation and derivative values' reliance on analyte concentration. The technological details are as follows:
- Techniques used derivative spectra
The method of derivative spectrophotometry is highly recognised for improving the resolution of overlapping spectra. Identifying a substance in the presence of another by selecting a wavelength where the signal from one chemical is negligible and the contribution from the other compound is strong is especially helpful. This method has been effectively used to identify a wide range of pharmaceuticals and element mixes, as well as individual medications and their breakdown products.
Unfortunately, recent attempts to assess medicines directly using traditional derivative techniques on first, second, third, and fourth order absorption spectra or ratio spectra have not always shown appropriate results in some medication combinations. In order to minimise noise, this problem requires developing techniques that entail mathematical modification of the derivatized spectra at the lowest order of derivatization. Notwithstanding these difficulties, derivative spectrophotometry upholds the essential tenets of classical spectrophotometry, including the law of additivity and the dependence of the derivative value on analyte concentration. The following is a summary of these techniques:
1] Subtraction of amplitude (AS)
This method seeks to reduce the number of steps by using a simplified version of the two-regression equation methodology. The projected value at this wavelength can be obtained by using the preceding calculation after noting the mixture's peak amplitude at ?2. The peak amplitude of drug (X) can therefore be found by subtracting the measured peak amplitude of the mixture at ?1 from the expected value at the same wavelength.
2] Modified subtraction of amplitude
We select one of the following wavelengths (e.g. ?1) because this specific technique is utilized for mixtures of two substances (X and Y) where the specific peak of the derivative spectrum of substance (X) coincides with the peak of substance (Y) at the same wavelength. Previously, spectrophotometric techniques were used to calculate the concentration of X. The matching Y can be obtained by subtracting this greatest amplitude from the mixture's maximum amplitude observed at ?1.
3] The Amplitude - Summation Technique (A-Sum)
When X and Y are combined, this new technique is applied when the initial difference spectrum (D) of Y indicates no contribution from The plot amplitude of Y in the ? isomixture can be subtracted from the measured amplitude corresponding to the total (X + Y) to determine the amplitude related to X. This can be done by computing the first derivative spectra (D) of the identical concentrations, assuming that X and Y interact at ? iso.
- Techniques based on the ratio spectrum's amplitude difference
- Ratio Difference Spectrophotometric Method (RDSM)
Since its development by Lotfy and Hegazy, the ratio difference spectrophotometric technique (RDSM) has proven useful in the investigation of binary and ternary mixtures after resolution. This method is predicated on the notion that the amplitude difference between two locations on the ratio spectra of a mixture directly correlates with the concentration of the target component, which stays independent of the interfering component.
- The CCSM, or Constant Center Spectrophotometric Method
Two further phases of the constant technique are constant equation and constant calculation utilizing the amplitude difference approach. By splitting the mixture's spectrum and using X or Y as the divisor, the procedure separately determines two factors (X and Y) in the first stage of the calculation, known as continuous computation. The constant value is multiplied by the appropriate divisor in the second stage of continuous multiplication to yield the zero-order absorption spectrum of X or Y (first spectrum). Regression analysis can be used to determine the concentration of X or Y by expressing the relationship between the absorbance values of the zero-cut curve of ?max.
- CC-SS, or Constant Center Coupled with Spectrum Subtraction
When there is only one distribution and Y is determined by the median, this new approach can be applied to binary combinations. By subtracting the Y spectrum from the combined (X + Y) spectrum, the spectral subtraction approach yields the zero-order spectrum of X, which can be used to find the X component. The regression equation that was utilized to find X is obtained by plotting the average absorbance value of the zero-biased absorption spectrum at ?max of X versus integration.
4. CV-AD, or Constant Amplitude Difference Method
A novel technique that has been employed is the Constant Amplitude Difference Method (CV-AD), which is derived from the Constant Center Method and the Center Amplitude Method. This method can be used to find a drug's zero-direction absorption spectrum. When a mixture of X, Y, and Z is employed, the Z concentration can be calculated using the arithmetic mean of a constant; where Y and Z have a longer range than X and significantly overlap. Concentration: Z concentration and Z ratio spectrum / Z' amplitude relationship quality.
- Constant Value (CV)
Constant value (CV) method: There are two extra phases in the constant value method. A recent application is the analysis of binary and ternary mixtures. This method concentrates on Z's analysis in the ternary combination of X, Y, and Z because Z is longer than Y and X. Next, ascertain the Z concentration in the continuous region where X and Y are zero using the regression equation. It accomplishes this by connecting the corresponding Z concentration to the amplitude of the Z/Z' ratio spectrum.
- The Amplitude Center Method (ACM)
By comparing amplitudes in the same ratio spectrum, the Center of Amplitude Method (ACM) employs a divisor to gradually identify each of the three components in a ternary mixture. Three more processes in this procedure are amplitude extraction, amplitude factor calculation, and amplitude calculation. These techniques are all described in detail for the examination of binary mixtures. The ternary mixture analysis technique that integrates three concepts at once is the fundamental amplitude method. Ternary mixes of Z, X, and Y with some or large spectra overlap can be treated with this innovative method. As an illustration, all spectra overlap at ?3, but only the Y and Z spectra overlap at ?1 and ?2 without the help of X.
- Method Based on Modulation of the Amplitudes of Ratio Spectra
- Method of Amplitude Modulation (AM)
The normalized spectrum of the divider can be used to change the sample ratio in the Amplitude method Modulation (AM) technique by dividing the specific spectrum of a component by its concentration [13, 14]. By dividing the spectrum by the continuous product's absorbance curve in a binary mixture—where one product is more continuous than the other and both exhibit equivalent results in the zero-level spectrum—the amplitude is regulated by concentration. Absorption points (in the ratio spectrum, represented as isobortive points).
- Advanced Amplitude Modulation Method (AAM)
When binary mixtures with significantly overlapping spectra are involved, and there is an isoabsorption point in the zero spectrum for each component, the Advanced Amplitude Modulation Method (AAM) expands the use of AM. There are two methods for figuring out the two components' concentrations. In the first method, the iso-point regression equation is used to determine both components after the isosbestic point and another point on the ratio spectrum are mathematically calculated to determine their difference. The second strategy combines the constant centre method with the AM method. This method begins by utilising a normalised concentration of one component as a divisor to calculate the variation in the ratio amplitudes of two selected wavelengths (?iso and ?2, where both spectra overlap) for varying concentrations of the same component. The iso-point regression equation is then used to determine both components.
- Induced Amplitude Modulation Method (IAM)
A different and innovative method for determining component concentrations in mixes with substantially or partially overlapping spectra is the Induced Amplitude Modulation (IAM) method. This technique deals with situations where X and Y show low absorptivity isoabsorption points or no isoabsorption points at all, which can cause mistakes when determining concentrations using AM or AAM. The initial step in the IAM method is the constant centre method, which involves using a normalised concentration of X' as a divisor to compute The link between the amplitude ratio of the difference between the pure Y of two chosen wavelengths (where ?2 is the wavelength at which the two spectra overlap and Pmax is the wavelength with the largest amplitude value in the ratio spectrum) is represented by the regression equation. Next, the analysis is done with Y's relative amplitude at ?max.
- Geometrical Amplitude Modulation Method (GAM)
Lotfy et al. invented the geometric amplitude modulation method (GAM). Ascertain the element (X) concentration when element (Y) is present. The procedure is predicated on a regression equation that illustrates the geometric effects of standard addition of X on the response of a binary mixture (X and Y). Using the normalized spectrum of Y as a divider, two places (P1 and P2) in the overlapping region of the X and Y ratio are chosen.
The regression equation can be used to express the relationship between the geometric shape of ?P and increasing X concentration (C_x addition) by computing the difference (?P = P1 - P2). By logging the constant value (Pconst) in the continuous region of Y, AM technology may ascertain the critical point (Y) directly.
- Techniques Using Mean Cantering of Ratio Spectrum Amplitudes
- Method of Mean Cantering of Ratio Spectra
Without any prior separation, this approach can be used to determine both binary and ternary combinations. First, ratio spectra are acquired; these spectra are mean centred to eliminate the constant. An extra step is carried out for ternary mixtures: the second ratio spectra are mean-centered after the mean-centered ratio spectra of the first two components are divided by their mean-centered vector.
- Utilising the Geometric Mean for Mean Centering
Using the geometric mean rather than the arithmetic mean to transform the data in the mean centering of ratio spectra method is an innovative approach. This method entails taking the logarithm of each data point prior to processing, and is thought to provide a more accurate assessment of central tendency.
- Algorithm for Pure Component Contribution (PCCA)
An innovative technique for separating the contributions of components from signals with significant overlap is the Pure Component Contribution Algorithm (PCCA). By employing mean centering as a processing tool, it creates a code function that removes the signal of interfering components and extracts the pure contribution of each component. This algorithm makes it possible to determine each component separately.
- Wavelet Transform Continuous (CWT)
Another technique for manipulating ratios is the wavelet transform, specifically the Continuous Wavelet Transform (CWT). While Fourier transform uses trigonometric functions (sine and cosine), this potent tool for signal processing includes several basic functions termed wavelets. Data compression, denoising, smoothing, and quantitative system analysis are among the uses of CWT. The wavelet transform is a rich set of elementary wavelets that can resolve a wide range of chemical issues by selecting the right measurement parameter.
- Conditions and Applications
The components' spectral characteristics determine how these strategies should be applied. Each method's benefits and drawbacks are outlined in the corresponding tables, which also offer suggestions for how best to use them depending on the type of spectrum data.
Instrumentation
1] Source
2] The Monochromator
3] The Cuvette
4] The Detector
5] The Amplifier and recorder
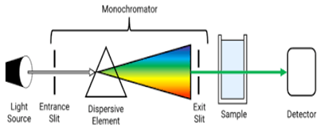
Figure 3 Instrumentation of UV
1] UV Sources:
A constant source of radiation that emits light at many wavelengths is necessary for vis spectroscopy. Several kinds of lamps are frequently utilised as UV radiation sources, including:
1.Hydrogen Lamp: This type of lamp generates ultraviolet light by igniting hydrogen atoms within a discharge tube. It mostly emits in the ultraviolet spectrum.
2. Deuterium Lamp: Using a discharge tube to excite deuterium atoms, this lamp creates UV light. It offers a spectrum that is continuous from ultraviolet to visible wavelengths.
3.Tungsten Lamp: Also referred to as an incandescent light, this type of light emits light in the visible and near-infrared regions, but not usually in the ultraviolet. It's not utilised for UV-Vis, but it is occasionally used for visible spectroscopy.
4. Xenon Discharge Lamp: Radiates in a wide range of wavelengths, from ultraviolet to near-infrared. Because of its UV emission, it is especially helpful for UV-Vis spectroscopy.
These lamps are essential to UV-Vis spectroscopy because they supply the radiation required to analyse things according to how much UV and visible light they absorb. Every kind of bulb has benefits, and the ones that are selected depend on the particular needs of the analysis.
A monochromator is an essential part of spectrophotometers and other optical devices that analyse light wavelengths. It operates by picking a certain wavelength from a light source that is polychromatic, or has several wavelengths. Here is a breakdown of its parts and how it works:
Operation of a Monochromator:
1.Entrance Slit: Through the entrance slit, polychromatic light of various wavelengths enters the monochromator.
2. Collimating Lens: The light enters and is collimated, or made parallel, by means of a lens. By taking this step, the light beams are guaranteed to be directed uniformly towards the dispersion element.
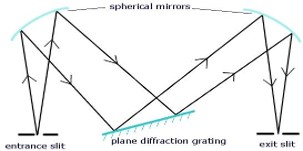
3. Dispersing Device (Prism or Grating): After collimated light has passed through a prism or diffraction grating, it comes into contact with a dispersing element. This part divides the incoming light into its individual wavelengths according to their various diffraction patterns or refractive indices.
4. Focusing Lens: The dispersed wavelengths are focused into the exit slit using a focusing lens following dispersion.
5. Exit Slit: The exit slit is positioned to let through a limited spectrum of light. Certain wavelengths can be chosen by varying the dispersing element or the exit slit. With the exit slit, the radiation currently emanating is monochromatic, i.e., it is limited to a single wavelength or a restricted range of wavelengths.
Sample Cell in UV Spectroscopy:
1.Openness Requirement: The sample and reference solutions must be contained in UV-transparent cuvettes. Because of its transparency, the incident UV radiation can travel through the solution without being significantly absorbed or distorted, which guarantees reliable absorbance measurements.
2. Materials Used: Quartz or Fused Silica Cuvettes: Because of their great transparency in the UV region, which is usually between 350 and 200 nm, these materials are preferred for UV spectroscopy. Due to their low UV absorption, quartz and fused silica reduce interference with the sample's absorption spectra during analysis.
3. Silicate Glasses: While quartz and fused silica are excellent materials for UV measurements, silicate glasses can also be utilised to make transparent cuvettes that span a larger range of light spectrums, including visible and UV. In spectroscopic applications, where measurements may range from UV to visible wavelengths, this permits flexibility.

Figure 4 sample solution filled in cavate
The detector is essential to UV-visible spectroscopy because it transforms light energy into electrical signals that can be analysed. The following explains chromophores and detectors:
Detector in UV-Visible Spectroscopy
1.Photodetector: A semiconductor device intended for reverse bias operation, a photodetector is usually a P-N junction diode. Photons from the incident light cause electron-hole pairs to form in the semiconductor material of the diode. Electrical current or voltage is produced as a result of this process, and it is proportionate to the intensity of the incident light.
2.Barrier Layer Cell (Photovoltaic Cell): Using the photovoltaic effect, this kind of detector directly transforms light into electrical energy. When exposed to light, it produces a voltage and is frequently found in solar cells and certain UV-visible spectrometers.
3. Photoemissive tubes, or phototubes : The photoelectric effect, which occurs when photons impact a photocathode and cause it to release electrons that are propelled towards an anode and produce an electrical signal, is the basis for how phototubes work. These are sensitive detectors that are employed in many different fields, including as spectroscopy.
4. Photomultiplier Tube: A very sensitive detector that increases the photocurrent that incident photons produce is called a photomultiplier tube (PMT). Its sensitive spectroscopic observations are made possible by its ability to detect extremely low light levels. It is composed of a photocathode, dynodes, and an anode.
Uv Visible Spectroscopy Application
UV-Vis spectroscopy is a flexible analytical method that is extensively applied in many different domains for both qualitative and quantitative chemical analysis. An outline of its uses is provided below:
1. Qualitative Analysis:
Elucidation of Organic Compounds: Based on their distinctive absorption bands, functional groups or chromophores within organic compounds can be identified with the use of UV spectroscopy. Certain absorption peaks at certain wavelengths can reveal information about the structure of organic materials, whether they are present or absent.
Impurity Detection: By observing extra absorption bands that deviate from the spectra of the primary chemical, UV-Vis spectroscopy can identify impurities in samples.
2. Quantitative Assessment:
Calculating Concentration of Compound: Based on Beer's law, which states that absorbance (A) is directly proportional to concentration (c) and path length (b) of the sample, UV-Vis spectroscopy is frequently employed for quantitative analysis:
A=?bc Where
b = Path length
ccc = Concentration
?\epsilon? = Molar absorptivity coefficient
AAAA = Absorbance
Acids and Bases' Dissociation Constants: By tracking variations in absorbance at various pH levels, UV spectroscopy can identify the dissociation constants (pKa) of acids and bases.
DNA Quantification and Thermal Denaturation:
By tracking variations in absorbance, a characteristic of nucleic acids, UV spectroscopy is used to measure and investigate the thermal denaturation of DNA.
- Determination of Configurations and Isomers:
• Geometrical Isomers: Variations in their absorption spectra allow UV spectroscopy to differentiate between geometrical isomers.
• Conjugated vs. Non-Conjugated Compounds: Conjugated systems can be distinguished from non-conjugated compounds by their distinctive absorption patterns.
• Axial vs. Equatorial Conformation: UV spectroscopy can occasionally distinguish between several molecular conformations based on their UV spectra.
CONCLUSION
Due to its capacity to yield both qualitative and quantitative information on chemicals, UV-Vis spectroscopy is indispensable in analytical laboratories. It finds use in biochemical research, materials science, medicinal analysis, and environmental monitoring. The method's sensitivity, usability, and versatility make it a mainstay in scientific analysis and research. UV spectroscopy has seen tremendous breakthroughs in the last ten years (2006-2016), which have completely changed the way analytical chemistry uses it. At the beginning of the decade, derivative spectrophotometry was the predominant method in the area; nevertheless, throughout time, new and creative spectrophotometric techniques have emerged. Because they do not use hazardous solvents or chemical reagents, these more recent techniques are efficient, economical, and environmentally friendly. These developments have resulted in the creation of techniques that can precisely and accurately analyse medication combinations seen in pharmaceutical formulations. These approaches are therefore starting to be seen as respectable substitutes for more intricate and resource-intensive hyphenated analytical procedures.
REFERENCE
- Jeffery GH, Bassett J, Mendham J, Denney RC. Vogel’s textbook of quantitative chemical analysis. Edition: 5th, ELBS with long man, Singapore, 3-11.
- Beckett & Stenlake Practical pharmaceutical chemistry Fourth Edition,1995.
- Donald L, Pavia, Gary M, Lampman, George S, Kriz Iames R et al. Spectroscopy. Third Edition, CBS Publishers and Distributors, 1997.
- Rifino CB. Pharmaceutical Process Validation, Switzerland, Edition,2003:2:1-43.
- International Conference on Harmonization (ICH), Validation of Analytical Procedures: Text and Methodology Q2 (R1), 2005.
- Patel D, Panchal D, Patel K. prof Dalwadim, Dr Upadhyay U. Review on uv visible spectroscopy. International Journal of Creative research Thoughts (IJCRT),2022:(10):2320-2882.
- UV-spectrophotometric method for simultaneous Estimation of metoprolol and amlodipine in bulk and Their formulation. International Journal of Biological & Pharmaceutical Research,2011:2(2):50-54.
- Brown, Chris W. "Ultraviolet, visible, near-infrared spectrophotometers. Ewing’s Analytical Instrumentation Handbook, Fourth Edition. CRC Press,2019:117-128.
- Verma, Govinda, Manish Mishra. “Development and optimization of UV-Vis spectroscopy-a review.” World Journal of Pharmaceutical Research,2018:7(11):1170- 1180.
- Modern Chemical Techniques, Ultraviolet/visible Spectroscopy, The Royal Society of Chemistry,102,103.
- Donald L. Pavia Gary M. Lampman, George S, Kriz Iames R, Vijaan. Spectroscopy. Third Edition, CBS Publishers, and Distributors, 1997.
- Skoog DA, Holler FJ, Nieman DA. Introduction to UV Spectroscopy in, principle of Instrumental analysis, 5thed., Cole publication, 2004.
- Sharma YR. Ultraviolet and visible spectroscopy in; Elementary Organic spectroscopy, 1Ed., S. Chand & Company Ltd., New Delhi, 2004, 9-60.
- Dr Khunt RC. Organic spectroscopy. international publisher, 2016.
- Chatwal GR SK. Anand Instrumental methods of chemical analysis, Himalaya Publishing House, 1979.
- Harvey D. Modern analytical chemistry. United States of America: McGraw-Hill; 2000.
- Hollas JM. Modern Spectroscopy. 4th Editon. UK: Wiley; 2004. p. 452.
- Andrews DL. Molecular photophysics and spectroscopy. UK: Morgan and Claypool; 2014. p. 94.
- Kenkel J. Analytical chemistry for technicians. Third ed. Greencastle, Ireland.: CRC Press; 2003. p. 584
- Raghubabu K, Mohan N, Kalyanaramu B, Ramdas C, Rao MN. Development of new visible spectrophotometric determination of tiaprofenic acid in bulk and formulations. Asian J Pharm Clin Res 2013;6:77-9.
- Sreeja U, Gurupadayya B, Chandan R. Novel spectrophotometric methods for the quantification of desvenlafaxine In pure and pharmaceutical dosage form. Asian J Pharm Clin Res 2015;8:267-70
- Naga Raju K, Sunitha T, Sudheer Babu I. Quantitative estimation of riluzole using solubilizing agent by UVspectrophotometry. Int J Appl Pharm 2014;6:4-5.
- Lotfy HM, Saleh SS, Hassan NY, Salem H. Novel two wavelength spectrophotometric methods for simultaneous determination of binary mixtures with severely overlapping spectra. Spectrochim Acta, Part A 2015;136:1786–96.
- Bindaiya S, Bankey S, Jain D. Simultaneous determination of nitazoxanide and ofloxacin in tablet by ultraviolet spectrophotometry (dual wavelength method). Int J ChemTech Res 2010;2:11-5.
- Ramadan NK, Mohamed HM, Moustafa AA. Simultaneous determination of rabeprazole sodium and domperidone. J Appl Pharm Sci 2011;1:73-80
- Prajapati J, Patel M, Prajapati R, Prajapati N. Simultaneous determination of Perindopril erbumine and Amlodipine besylate by absorption factor method. Int J Appl Biol Pharm Technol 2011;2:230-3.
- Patel CV, Khandhar AP, Captain AD, Patel KT. Validated absorption factor spectrophotometric and reversed-phase high-performance liquid chromatographic methods for the determination of ramipril and olmesartan medoxomil in pharmaceutical formulations. Eurasian J Anal Chem 2007;2:160-71.
- Lotfy HM, Hegazy MA, Rezk MR, Omran YR. Novel spectrophotometric methods for simultaneous determination of timolol and dorzolamide in their binary mixture. Spectrochim Acta Part A 2014;126:197-207.
- Lotfy HM, Saleh SS, Hassan NY, Salem H. A comparative study of novel spectrophotometric methods based on isosbestic points; application on a pharmaceutical ternary mixture. Spectrochim Acta Part A 2014;126:112–21.
- El-Ghobashy MR, Abo-Talib NF. Spectrophotometric methods for the simultaneous determination of a binary mixture of metronidazole and diloxanide furoate without prior separation. J Adv Res 2010;1:323-9.
- Lotfy HM, Hassan NY, Elgizawy SM, Saleh SS. Comparative study of new spectrophotometric methods; an application on a pharmaceutical binary mixture of ciprofloxacin hydrochloride and hydrocortisone. J Chil Chem Soc 2013;58:1651-7.
- Lotfy HM, Hegazy MA, Rezk MR, Omran YR. Comparative study of novel versus conventional two-wavelength spectrophotometric methods for analysis of spectrally overlapping binary mixture. Spectrochim Acta Part A 2015;148:328-37.
- Samir A, Salem H, Abdelkawy M. New developed a spectrophotometric method for simultaneous determination of salmeterol xinafoate and fluticasone propionate in bulk powder and seritide diskus inhalation. Bull Fac Pharm Cairo Univ 2012;50:121-6.
- Salem H, Lotfy HM, Hassan NY, El-Zeiny MB, Saleh SS. A comparative study of different aspects of manipulating ratio spectra applied for ternary mixtures: derivative spectrophotometry versus wavelet transform. SpectrochimActa Part A 2015;135:1002-10.
- Ghorpade SA, Sali MS, Kategaonkar AH, Patel DM, Choudhari VP, Kuchekar BS. Simultaneous determination of emtricitabine and tenofovir by the area under the curve and dual wavelength spectrophotometric method. J Chil Chem Soc 2010;55:115-7.
- Abdelrahman MM. Simultaneous determination of cinnarizine and domperidone by the area under the curve and dual wavelength spectrophotometric methods. Spectrochim ActaPart A 2013;113:291-6.
- Lotfy HM, Saleh SS, Hassan NY, Salem H. Computation of the geometric representation of novel spectrophotometric methods used for the analysis of minor components in pharmaceutical preparations. Spectrochim Acta Part 2015;151:628-43.
- Erk N. Analysis of binary mixtures of losartan potassium and hydrochlorothiazide by using high-performance liquid chromatography, ratio derivative spectrophotometric and compensation technique. J Pharm Biomed Anal 2001;24:603–61.
- Lotfy HM, Saleh SS, Hassan NY, Elgizawy SM. Spectrophotometric and chromatographic methods for the determination of a binary mixture of sodium cromoglicate and xylometazoline hydrochloride. Anal Chem Indian J 2013;13:152-60.
- Samir A, Lotfy HM, Salem H, Abdelkawy M. Development and validation of simultaneous spectrophotometric and TLCspectro- densitometric methods for determination of beclomethasone dipropionate and salbutamol in combined dosage form. Spectrochim Acta Part A 2014;128:127–36.
- Mohamed ME. First-derivative spectrophotometric determination of a mixture of pirbuterol hydrochloride and butorphanol tartrate. Anal Lett 1986;11:1323-39.
- Hassan SM, Amer SM, Amer MM. Determination of fusidic acid and sodium fusidate in pharmaceutical dosage forms by firstderivative ultraviolet spectrophotometry. Analyst1987;112:1459-61.
- Ouanes S, Kallel M, Trabelsi H, Safta F, Bouzouita K. Zerocrossing derivative spectrophotometry for the determination of haloperidol in the presence of parabens. J Pharm Biomed Anal 1998;17:361-4.
- El-Gindy A, Ashour A, Abdel-Fattah L, Shabana MM. First derivative spectrophotometric, TLC-densitometric, and HPLC determination of acebutolol HCL in the presence of its acidinduced degradation product. J Pharm Biomed Anal 2001;24:527–34.
- Lotfy HM, Tawakkol SM, Fahmy NM, Shehata MA. Validatedstability indicating spectrophotometric methods for the determination of lidocaine hydrochloride, calcium dobesilate, and dexamethasone acetate in their dosage forms. Anal ChemLett 2013;3:208-25.
- Yehia AM, Abd El-Rahman MK. Application of normalized spectra in resolving a challenging orphenadrine and Paracetamol binary mixture. Spectrochim Acta Part A 2015;138:21-30.
- Wahbi AAM, Abdel-Razak O, Gazy AA, Mahgoub H, Moneeb MS. Spectrophotometric determination of omeprazole, lansoprazole and pantoprazole in pharmaceutical formulations. J Pharm Biomed Anal 2002;30:1133-42.
- Lotfy HM, Tawakkol SM, Fahmy NM, Shehata A. A comparative study of novel spectrophotometric resolution techniques applied for pharmaceutical mixtures with partially or severely overlapped spectra. Spectrochim Acta Part A 2015;136:937–52.
- Lotfy HM, Tawakkol SM, Fahmy NM, Shehata MA. Successive spectrophotometric resolution as a novel technique for the analysis of ternary mixtures of pharmaceuticals. SpectrochimActa Part A 2014;121:313–23.Lotfy HM,
- Fayez YM, Michael AM, Nessim CK. Simultaneous determination of mebeverine hydrochloride and chlordiazepoxide in their binary mixture using novel univariate spectrophotometric methods via different manipulation pathways. Spectrochim Acta Part A 2016;155:11-20.
- El-Bardicy MG, Lotfy HM, El-Sayed MA, El-Tarras MF. Smart stability-indicating spectrophotometric methods for determination of binary mixtures without prior seption. J AOAC Int 2008;91:299-310.
- Lotfy HM, Hagazy MA. Comparative study of novel spectrophotometric methods manipulating ratio spectra; an application on a pharmaceutical ternary mixture of omeprazole, tinidazole, and clarithromycin. Spectrochim ActaPart A 2012;96:259–70.
- Lotfy HM, Hegazy M. Simultaneous determination of some cholesterol-lowering drugs in their binary mixture by novel spectrophotometric methods. Spectrochim Acta Part A 2013;113:107-14.
- Lotfy HM. Determination of simvastatin and ezatimibe in combined tablet dosage forms by constant center spectrophotometric method Int J Pharm Pharm Sci 2012;4:673-9.
- Saleh SS, Lotfy HM, Hassan NY, Salem H. A comparative study of progressive versus successive spectrophotometric resolution techniques applied for pharmaceutical ternary mixtures. Spectrochim Acta Part A 2014;132:239–48.
- Lotfy, H. M., Saleh, S. S., Hassan, N. Y., & Elgizawy, S. M. (2013). Univariate versus Multivariate Spectrophotometric Methods for Simultaneous Determination of Complex Binary Mixtures with Overlapped Spectra: A Comparative Study. Analytical Chemistry Letters, 3(2), 70–84


 Lalit R. Gaikwad *
Lalit R. Gaikwad *
 Rupesh D. Gaikwad
Rupesh D. Gaikwad
 Jagruti V. Gavit
Jagruti V. Gavit
 Vaibhavi S. Kadam
Vaibhavi S. Kadam
 Lina H. Thakare
Lina H. Thakare






 10.5281/zenodo.13095212
10.5281/zenodo.13095212